【LGR-093】洛谷 10 月月赛 I & MCOI R6 Div.2 A&B

赛事链接：https://s.heyiqi.cc/g67

【A】T173758 「MCOI-06」Flight

题目描述
书虫需要移动他的盾构机。

书虫将 MC 空间抽象为二维平面。他的盾构机现在在 (a,b)(a,b)，而书虫想把盾构机移动到 (c,d)(c,d)。

书虫每一步可以将盾构机向东南西北任何方向行动。但是这盾构机有一个限制：相邻两步不能向同一个方向走！

给定 (a,b)(a,b) 和 (c,d)(c,d)，请计算书虫最少需要几步将盾构机移动到终点。

求书虫的最少步数。可以证明，他永远可以到达终点。

输入格式
本题有多组数据。

第一行一个正整数 T，表示表示数据的组数。

接下来 T 行，每行四个整数 a,b,c,d ，代表一组数据，其中 (a,b) 为起点，(c,d) 为终点。

输出格式
输出 T 行，第 i 行代表第 i 组数据的答案。

输入输出样例
输入#1

3
-2 0 -2 1
0 1 3 3
-1 1 1 1

输出#1

1
5
4

说明/提示
样例 1 解释

• 对于第一组，最优策略为 (-2,0)->(-2,1)。
• 对于第二组，最优策略为 (0,1)->(1,1)->(1,2)->(2,2)->(2,3)->(3,3)。
• 对于第三组，最优策略之一为 (-1,1)->(0,1)->(0,0)->(1,0)->(1,1)。

数据规模与约定
本题采用捆绑测试。

• Subtask 1（29 pts）：0<=a,b,c,d<=3。
• Subtask 2（29 pts）：a=c。
• Subtask 3（42 pts）：无特殊限制。
  对于所有数据，1<=T<=10^5，|a|,|b|,|c|,|d|<=10^18 。

分析

通过观察可以发现，如果起点和终点在对角线上时，需要走的步数为2*|X1-X2|(X1>=X2)步，而两点在直线上时需要走的步数为2*(X1-X2)+(-1)^(X1-X2)(X1>=X2，水平) 或 2*(Y1-Y2)+(-1)^(Y1-Y2)(Y1>=Y2，垂直)，因此我们可以先走到与终点水平或垂直的直线上，再根据在直线上的规律走到终点（相距n步：n为奇数时，2n-1步；n为偶数时，2n步）。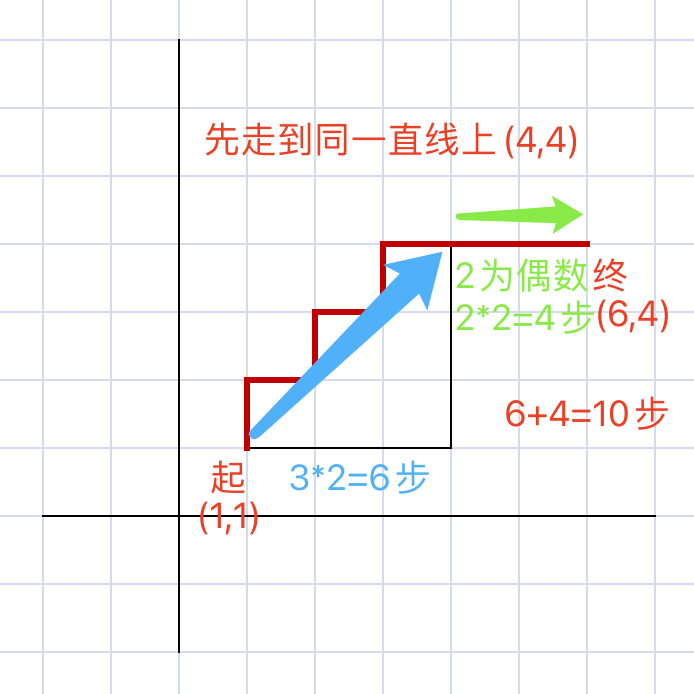

代码

//
// Created by 何艺麒 on 2021/10/1.
//

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;

int main() {
    int t;
    cin >> t;
    while (t--) {
        ll a, b, c, d;
        cin >> a >> b >> c >> d;
        ll pub = min(max(a, c) - min(a, c), max(b, d) - min(b, d));
        ll oth = max(max(a, c) - min(a, c), max(b, d) - min(b, d)) - pub;
        cout << pub * 2 + (oth & 1 ? 2 * oth - 1 : 2 * oth) << endl;
    }
    return 0;
}

【B】T173727 「MCOI-06」Gerrymandering

题目描述
给定正整数 n,m,k 能否将一个 n×m 表格染色，使得每一个颜色形成恰好一个连通块，并且每一个连通块大小为 k ？

如果存在，请构造一个合法方案。

输入格式
本题有多组数据。
第一行一个正整数 T，表示表示数据的组数。
接下来 TT 行，每行三个正整数 n,m,k。

输出格式
输出 T 行，第 i 行含第 i 组数据的答案。如果存在，输出 YES，否则，输出 NO 。
如果存在，接下来输出 n 行，其中每行 m 个正整数，其中每一个正整数小于等于 10^9 并且形成一个大小恰好为 k 的连通块。

输入输出样例
输入#1

3
3 3 3
3 3 33
6 6 4

输出#1

YES
1 1 2
1 2 2
3 3 3
NO
YES
1 1 2 2 3 3
1 2 2 4 4 3
1 5 5 4 6 3
5 5 7 4 6 6
8 7 7 7 9 6
8 8 8 9 9 9

说明/提示
样例 1 解释
数据组 3 的合法输出之一：

数据规模与约定
本题采用捆绑测试。

Subtask 1（20 pts）：k=1 。
Subtask 2（30 pts）：n=1 。
Subtask 3（50 pts）：没有特殊限制。
对于 100% 的数据，1<=n,m,k,T,∑nm<=10^6 。

分析

对于n*m%k==0的表格一定有解，模拟填充，第一行顺序填，第二行逆序填，以此类推（如下图），保证全都是连通块。

代码

//
// Created by 何艺麒 on 2021/10/1.
//

#include <bits/stdc++.h>

using namespace std;

int main() {
    int t;
    cin >> t;
    while (t--) {
        int n, m, k;
        cin >> n >> m >> k;
        if (n * m % k != 0) {
            cout << "NO" << endl;
        } else {
            cout << "YES" << endl;
            bool seq = true;
            int cur = 1;
            int curCnt = 0;
            vector<vector<int>> ans(n, vector<int>(m, 0));
            for (int i = 0; i < n; i++) {
                if (seq) {
                    for (int j = 0; j < m; j++) {
                        ans[i][j] = cur;
                        if (++curCnt == k) {
                            ++cur;
                            curCnt = 0;
                        }
                    }
                } else {
                    for (int j = m - 1; j > -1; j--) {
                        ans[i][j] = cur;
                        if (++curCnt == k) {
                            ++cur;
                            curCnt = 0;
                        }
                    }
                }
                seq = !seq;
            }
            for (auto x: ans) {
                for (auto y: x) {
                    cout << y << " ";
                }
                cout << endl;
            }
        }
    }
    return 0;
}